5.1 Función Creciente y Decreciente.
Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x1 y x2, con la condición x1 £ x2, se verifica que
f( x1 ) < f( x2 ).
Se dice estrictamente creciente si de x1 < x2 se deduce que f(x1) < f(x2).

· Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x1 y x2, que cumplan x1 £ x2, entonces f(x1 ) ³ f(x2 ).
Siempre que de x1 < x2 se deduzca f(x1 ) > f(x2 ), la función se dice estrictamente decreciente.

Video de como hacer las funciones crecientes y decrecientes:
5.2 Extremos Relativos y Extremos Absolutos.
| Extremos relativos La función f tiene un máximo relativo al punto c si hay un intervalo (r, s) (aún cuando sea muy pequeño) conteniendo c para el cual f(c) ≥ f(x) para toda x entre r y s para la cual f(x) esté definida.  Un extremo relativo, significa un máximo relativo o un mínimo relativo. La siguiente gráfica muestra unos extremos relativos.  | Ejemplo Sea

|
| Extremos absolutosExtremos relativos a veces pueden ser extremos absolutos, como demuestra la siguiente definición: f tiene un máximo absoluto a c si f(c) ≥ f(x) para toda x en el dominio de f. f tiene un mínimo absoluto a c si f(c) ≤ f(x) para toda x en el dominio de f. La siguiente figura muestra dos extremos relativos que están también extremos absolutos.  | Ejemplo Sea otra vez

|
Video de como determinar Extremos Relativos y Extremos Absolutos:
5.3 Prueba de la Primera Derivada para la determinación de Máximos y Mínimos.
Note que f está definida para
Como
Los valores críticos son
Determinemos ahora cuándo
Como
 |
Como
La representación gráfica de la función es la siguiente:

|
Característica de una curva en el entorno de un punto en el que la tangente no la atraviesa. Se dice que dicha curva, en el punto dado, presenta una concavidad hacia el lado donde no se encuentra la tangente.
Concavidad es un concepto geométrico relacionado con el doblez de la gráfica de una función. La concavidad se toma positiva si el doblez es hacia arriba y negativa si el doblez es hacia abajo.
Prueba de la Segunda Derivada.
S o l u c i o n e s
 |  |
 | |
Video de como sacar la segunda derivada:
5.5 Optimización de funciones económico-administrativas:
maximización de funciones de ingreso, utilidad y beneficios; minimización de
funciones de costos y costos promedio.
FUNCIÓN INGRESO
CONCEPTO:
Los ingresos totales son el efectivo que el fabricante o el productor recibe por la venta de su producción. Relaciona a las cantidades vendidas por el precio de cada una de ellas, es decir:
Ingreso total = (precio por unidad).(número de unidades vendidas)
I(x) = p . q
El precio algunas veces lo rige el mercado, por lo cual se pude determinar que la variable “p” estará determinada por la función de demanda en el mercado, es decir:
Ingreso total = (función de demanda).(número de unidades vendidas)
I(x) = f(x) . q
De la función ingreso no se puede definir si es una función creciente o decreciente, ya que la misma está relacionada con la venta de unidades. Para determinar el ingreso promedio o ingreso medio, se deberá dividir el ingreso total por la cantidad vendida.

FUNCIÓN UTILIDAD:
Es decir, que una función de utilidad asigna valores numéricos (que se pueden denominar "utiles") a cada cantidad de bienes consumidos. Un valor mas elevado de la función de utilidad es preferido a un valor inferior.
En el siguiente gráfico, vemos un ejemplo de una función de utilidad:

Función Beneficio:
BENEFICIO = 25 X q- ( 1200 + 15 X q )
El ejercicio solicita el nivel de ingreso, o sea el beneficio, para a) 200, b) 300 o c) 100 unidades. Entonces sólo falta sustituir en esta expresión el valor de "q" y hacer las operaciones. Cuidado que los signos de "+" y "-" separan términos. Primero hay que multiplicar por "15" y luego sumarle "1200".
BENEFICIO (a) = 25 x 200 - (1200 + 15 x 200 )
BENEFICIO (a) = 5000 - (1200 + 3000)
BENEFICIO (a) = 5000 - (4200)
BENEFICIO (a) = 800. En resumen, la empresa gana 800 pesos.
Analogamente, para la segunda parte : BENEFICIO (b) = 25 x 300 - (1200 + 15 x 300 )
Entonces BENEFICIO (b) = 7500 - ( 1200+ 4500) = 1800 La empresa gana 1800 pesos.
Y para la tercera parte : BENEFICIO (c) = 25 x 100 - (1200 + 15 x 100 )
BENEFICIO (c) = 2500 - (1200 + 1500 )
BENEFICIO (c) = 2500 - 2700
BENEFICIO(c) = -200 La empresa pierde 200 pesos.

Función de Costos:
Una función costo especifica el costo C como una función de la cantidad de artículos x. En consecuencia, C(x) es el costo de x artículos, y tiene la forma Costo = Costo variable + Costo fijo
En la que el costo variable es una función de x y el costo fijo es constante. Una función costo de la forma: C(x) = mx + b
Se llama una función costo lineal; el costo variable es mx y el costo fijo es b. La pendiente, el costomarginal, mide el costo incremental por artículo.
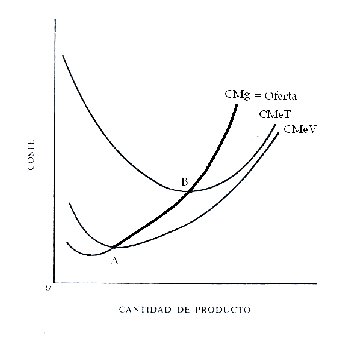
Costo Promedio:
4. Sea  , la función de costo total de producir y vender ropa para caballero, dada en miles de pesos y donde x es el número (en cientos) de prendas. Calcular el costo marginal y el costo promedio marginal para producir y vender la prenda 211.
, la función de costo total de producir y vender ropa para caballero, dada en miles de pesos y donde x es el número (en cientos) de prendas. Calcular el costo marginal y el costo promedio marginal para producir y vender la prenda 211.
Para obtener el costo marginal derivemos la función, esto es:
Ahora calcular el costo marginal para producir y vender la prenda 211, para lo cual se debe considerar que x es igual a2.1, dado que también x está en cientos de piezas, así:
Lo cual significa que existe una razón de cambio del costo total de 7.6 para cuando se produce y vende la prenda 211.
Obtener ahora la función de costo promedio, para lo cual dividiremos la función de costo total entre x:

Con esta función se debe calcular la función de costo promedio marginal; derivando ésta:

Esta razón de cambio por unidad es de 1.6395.
5.6 Elasticidades: elasticidad de la demanda y
elasticidad del ingreso.
Elasticidad.
Video de como realizar la función de demanda:
https://www.youtube.com/watch?v=fNzES1qMg7g
Video de como realizar la función de demanda:
https://www.youtube.com/watch?v=fNzES1qMg7g
Elasticidad de la Demanda:

Elasticidad de Ingreso:

Elasticidad de Ingreso:

Lo que aprendí en la Unidad 5°:
Por último durante esta unidad concluimos con el curso y lo último que vimos fueron las funciones crecientes y funciones decrecientes; aprendimos a obtener los extremos relativos y los extremos absolutos, aprendimos a usar la primera derivada para obtener máximos y mínimos, después de esto vimos la concavidad, los puntos de inflexión, y aprendimos a utilizar la segunda derivada y gracias a esto se puede obtener la concavidad y los puntos de inflexión de una función; vimos las funciones de ingreso, utilidad y beneficios, funciones de costos y costo promedio; y al final vimos el tema de la elasticidad en general y la elasticidad de la demanda y del ingreso.
