3.1 Definición de la Derivada.
La derivada de la función f(x) en el punto x = a es el valor del límite, si existe, de un cociente incremental cuando el incremento de la variable tiende a cero.


3.2 Diferenciación de Funciones por Incrementos.
Si f(x) es una función derivable, la diferencial de una función
correspondiente al incremento h de la variable independiente,
es el producto f'(x) · h.
La diferencial de una función se representa por dy.


Interpretación geométrica



La diferencial en un punto representa el incremento de la
ordenada de la tangente, correspondiente a un incremento de
la variable.
3.3 La Derivada como Razón de Cambio
Comenzando por la Razón Instantánea de Cambio de una función cuya variable independiente es el tiempo t. suponiendo que Q es una cantidad que varía con respecto del tiempo t, escribiendo Q=f(t), siendo el valor de Q en el instante t. Por ejemplo
- El tamaño de una población (peces, ratas, personas, bacterias,…)
- La cantidad de dinero en una cuenta en un banco
- El volumen de un globo mientras se infla
- La distancia t recorrida en un viaje después del comienzo de un viaje
El cambio en Q desde el tiempo t hasta el tiempo t+"t, es el incremento
La Razón de Cambio Promedio de Q (por la unidad de tiempo) es, por definición, la razón de cambio "Q en Q con respecto del cambio "t en t, por lo que es el cociente
Definimos la razón de cambio instantánea de Q (por unidad de tiempo) como el límite de esta razón promedio cuando "t!0. Es decir, la razón de cambio instantánea de Q es

Lo cual simplemente es la derivada f´(t). Así vemos que la razón de cambio instantánea deQ=f(t) es la derivada

3.4 Diferenciabilidad y Discontinuidad.
Derivada; Diferenciabilidad
La derivada de una función f en el punto a en su dominio se define por
| f'(a) | = | lim h | h |
Decimos que la función f es diferenciable en el punto a en su dominio si f'(a) existe.
Diferenciable en un subconjunto del dominio
La función f es diferenciable en el subconjunto S de su dominio si es diferenciable en cada punto de S.
La función f es diferenciable en el subconjunto S de su dominio si es diferenciable en cada punto de S.
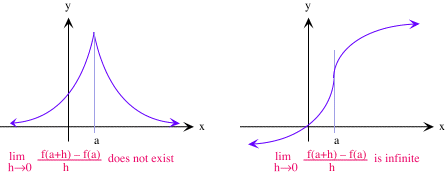
Nota
| Una función puede fallar ser diferenciable en el punto a si | lim h | h | no existe, o es infinito. |
En el primer caso, a veces tenemos una cúspide en la gráfica, y en el último caso, obtenemos un punto de tangencia vertical.
Si alguna de las tres condiciones continuidad de no se cumple, la función es discontinua en un punto.

La función es discontinua porque en x = 2 no existe imagen.


La función es discontinua porque en x = 2 no tiene límite,
ya que no coinciden los límites laterales..
3.5 Reglas básicas de derivación: la derivada de una
constante, de una constante por una función, de suma o resta de funciones, y
del producto o del cociente de funciones.
1° La Derivada de una Constante:
La derivada de una constante es cero.

Ejemplo


2° Derivada de una Constante por una Función.
La derivada del producto de dos funciones es igual al primer factor por la derivada del segundo más el segundo factor.

Derivada de una constante por una función
La derivada del producto de una constante por una función es igual al producto de la constante por la derivada de la función.

Ejemplos




3° Derivada de Suma y Resta de Funciones.
La derivada de una suma de dos funciones es igual a la suma de las derivadas de dichas funciones.
Esta regla se extiende a cualquier número de sumandos, ya sean positivos o negativos.

Ejemplos






Video Tutorial de Derivada de una Suma y Resta de Funciones: https://www.youtube.com/watch?v=6R_aS5lcZm4
4° Derivada de Multiplicaciones y Divisiones de Funciones.
La multiplicación de dos funciones f y g es otra función f ·g, cuyas imágenes se obtienen multiplicando
Si las funciones vienen definidas por una fórmula, la función resultante tiene como expresión analítica el
Por ejemplo, sean f(x) = x + 2 y g(x) = x2, entonces la función producto es
| |
 | |
 La división de dos funciones f y g es otra función f /g, cuyas imágenes se obtienen dividiendo las imágenes de f y g, siempre que la imagen de g sea distinto de 0.
Si las funciones vienen definidas por una fórmula, la función resultante tiene como expresión analítica la división de dichas fórmulas, excepto para los valores de x en que g(x) es cero, pues para dichos valores no existe la función división.
Sean f(x) =x3 + 2 y g(x) = x2. La función división f/g es:
El dominio de definición de esta función es R - {0}, es decir está definida para cualquier valor de x excepto para x = 0.
En la siguiente escena puedes ver las gráficas de estas tres funciones f(x) , g(x) y h(x) = f(x)/h(x).
3.6 La Regla de la Cadena y de la Potencia.
La regla de la cadena es la fórmula resultante de la derivada de la composición de funciones.
 Ejemplos       
Video acerca de la Regla de la Cadena:
Regla de la Potencia:
Regla de Potencias
La derivada de una potencia o función potencial, es igual al exponente por la base elevada al exponente menos uno y por la derivada de la base.
3.7 Aplicaciones a las ciencias económico administrativas: costo marginal, ingreso marginal, utilidad marginal, propensión marginal al consumo y propensión marginal al ahorro.
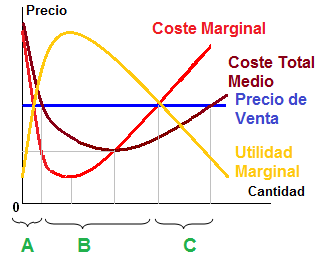
Costo Marginal:

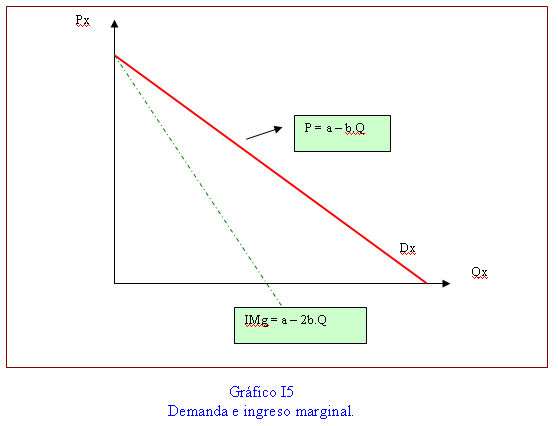
Ingreso Marginal:
Utilidad Marginal:
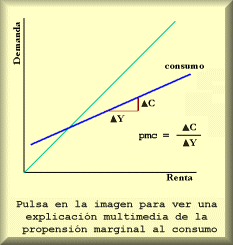
Propensión Marginal al Consumo y al Ahorro:
Lo que aprendí de la Unidad 3°:
Durante esta unidad vimos lo que era la derivada, hicimos diferenciación de funciones por incrementos; utilizamos a la derivada como razón de cambio; vimos lo que era la diferenciabilidad y la continuidad; aprendimos las reglas básicas de la derivada al realizar una suma o resta de funciones y también cuando se multiplican o se dividen funciones; vimos la regla de la cadena y de la potencia; y aprendimos a usarlas como en el costo marginal, el ingreso marginal, la utilidad marginal; y vimos la propensión al consumo y al ahorro.
| |



muy buen blog, buen trabajo
ResponderEliminarBuen blog
ResponderEliminar