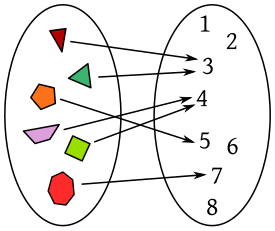
- Una FUNCIÓN es una regla que asigna a cada número de entrada exactamente un número de salida.
1.2 Dominio y Rango de una Función.
- El DOMINIO DE UNA FUNCIÓN, es el conjunto de números de entrada para los cuales se aplica la regla.
- El RANGO DE UNA FUNCIÓN, es el conjunto de todos los números posibles de
salida.
1.3 Tipos de Funciones.
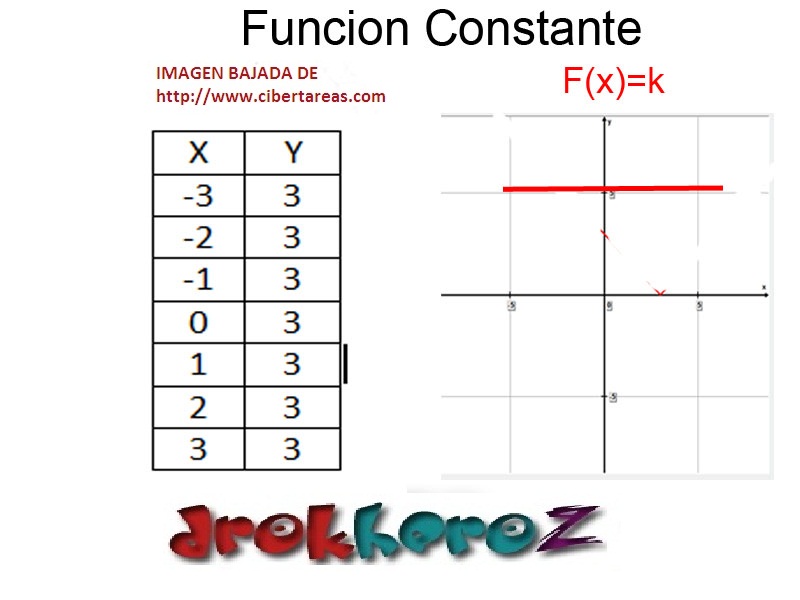
1. Función Constante.
Una función de la forma h(x)=c, donde c es una constante, se llama función constante. Una Función que siempre es constante. Dominio= IR.
2. Función Polinomial.
Aquella que depende de x que sus valores sean positivos con forma: f(x)= CnXn + Cn-1Xn-1 + ........ C1X + C0. Dominio= IR, donde:
n= grado de la función.
c= una constante.
x= variable independiente.

Función en donde está un polinomio entre otro polinomio. Dominio igualado a 0.
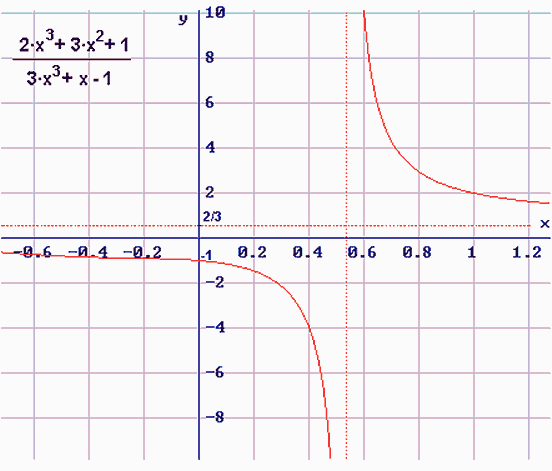
4. Función Radical.
Las funciones radicales, también conocidas como funciones irracionales; que como su nombre indica son aquella funciones en las que su definición aparece un radical, o lo que es lo mismo una raíz.

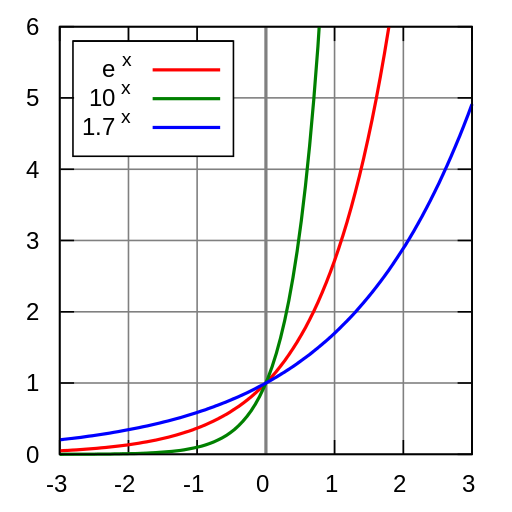
5. Función Exponencial.
Se llaman así a todas aquellas funciones de la forma f(x) = bx, en donde la base b, es una constante y el exponente la variable independiente. Cuando la variable esta en el exponente. Dominio IR.
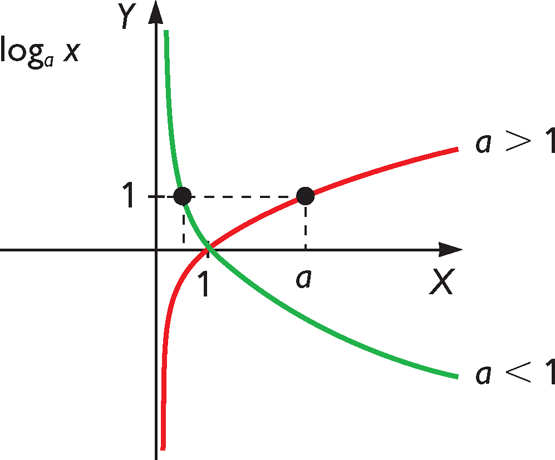
6. Función Logarítmica.
Una función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1, puesto que el resultado sería 0. Las que tienen logaritmos.
7. Funciones Trigonométricas.
Para las Funciones Trigonométricas, haremos uso del Teorema de Pitágoras y trabajaremos con las Funciones de Seno, Coseno y Tangente, y sus inversas, además de apoyarnos siempre con la Calculadora.

8. Funciones por Partes.
La cantidad que tenga va a tomar el valor o también son funciones definidas por distintos criterios, según los intervalos que se consideren.

Digamos que trabajas con las siguientes dos funciones.
La suma de las funciones puede escribirse como f(x) + g(x) o (f + g)(x). Observa lo que sucede cuando se suman estas dos funciones.
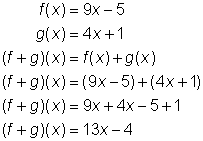
Y es todo, la suma de las dos funciones es la suma de los dos polinomios.
La suma, la resta, la multiplicación y la división se explicarán también. La tabla siguiente muestra la notación usada para cada tipo de operación aritmética.
Suma
| ||
Resta
| ||
Multiplicación
| ||
División
|
Ya viste un ejemplo de sumar dos funciones. Veamos otro ejemplo. El dominio (los valores de x) para ambas funciones es todos los números reales.
Ejemplo
| ||
Problema
|
Encontrar (f + g)(x).
| |
 |
Identifica f(x) y g(x). Reemplaza f(x) con
| |
Respuesta
| ||
La resta sigue el mismo proceso. Siempre y cuando te acuerdes de cómo restar un polinomio de otro, puedes restar una función de otra.
Ejemplo
| ||
Problema
|
Encontrar (g – f)(x).
| |
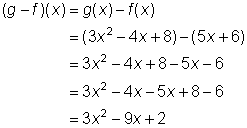 |
Reemplaza g(x) yf(x) con sus respectivas expresiones.
Luego suma y combina los términos semejantes.
| |
Respuesta
| ||
Ejemplo
| ||
Problema
| 
Encontrar (f – h)(x).
| |
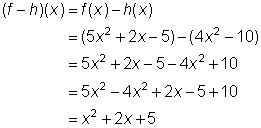 |
Observa que (f –h)(x)
= f(x) – h(x).
Puedes ignorarg(x) porque no se requiere resolver para este problema.
Reemplaza las notaciones de función con sus polinomios apropiados y resta.
| |
Respuesta
| ||
A)
B)
C)
D)
|
Multiplicar y dividir funciones también es como multiplicar y dividir polinomios. Revisa los siguientes ejemplos.
Ejemplo
| ||
Problema
|
Encontrar el producto de f yg.
| |
Para encontrar el producto, multiplica las funciones.
| ||
 |
Reemplaza f(x) con (2x + 1) y g(x) con (5x – 3).
| |
Respuesta
| ||
Ejemplo
| ||
Problema
| 
Encontrar
| |
 |
Para encontrar el cociente, divide fentre g.
Sustituye los polinomios por f(x) yg(x) y divide. Sumamos
Recuerda renombrar
| |
Respuesta
| ||
Las operaciones con tres funciones trabajan de la misma forma. En el ejemplo siguiente, dos funciones se suman y luego se dividen entre una tercera función. No es distinto de lo que ya has hecho con polinomios, sólo no dejes de sustituir los polinomios en las funciones correctas, combina, divide y simplifica.
Ejemplo
| |||
Problema
| 
Encontrar
| ||
 |
Reemplaza f(x), g(x) y h(x) con polinomios equivalentes. Sumamos
| ||
 |
Suma f(x) y g(x).
| ||
 |
Divide entre h(x). Saca el factor de 3x2del numerador y luego simplifica la expresión, usando
| ||
Respuesta
| |||
Video Tutorial de como se realizan Operaciones con Funciones:
1.5 Composición de Funciones.
Video Tutorial de Composición de Funciones:
1.6 Gráfica de una Función.
Función constante
y = n

Función identidad
f(x) = x

Función lineal
y = mx

Función afín
y = mx + n

Función cuadrática
f(x) = ax² + bx +c

Función parte entera de x
f(x) = E (x)

Función mantisa
f(x) = x - E (x)


Función signo
f(x) = sgn(x)


Función racional



Función exponencial


Función logarítmica


Función seno
f(x) = sen x

Función coseno
f(x) = cosen x

Función tangente
f(x) = tg x
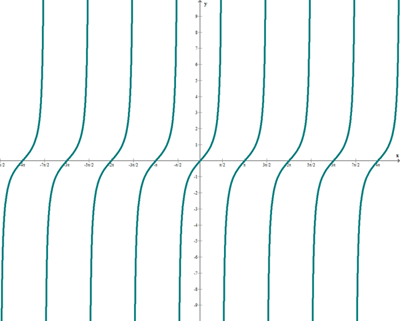
Función cotangente
f(x) = cotg x

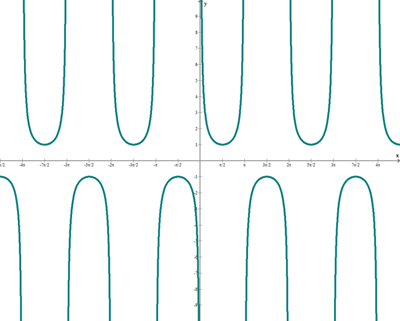
Función secante
f(x) = sec x
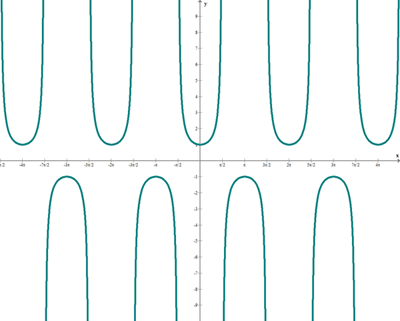
Función cosecante
f(x) = cosec x
Video Tutorial de Gráfica de una Función:
1.7 Función Lineal y Función Cuadrática.
Una Función f es una Función Lineal si y solo sí f(x) puede escribirse en la forma f(x)=ax+b, donde a y b son constantes y a no es igual a 0.
La función lineal es del tipo:
y = mx
Su gráfica es una línea recta que pasa por el origen de coordenadas.
y = 2x
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y = 2x | 0 | 2 | 4 | 6 | 8 |

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:
f(x) = ax2 + bx + c
donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero.
En la ecuación cuadrática cada uno de sus términos tiene un nombre.
Así,
ax2 es el término cuadrático
bx es el término lineal
c es el término independiente
Cuando estudiamos la ecuación de segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se dice que es unecuación completa, si a la ecuación le falta el término lineal o el independiente se dice que la ecuación es incompleta.
Representación gráfica de una función cuadrática
Si pudiésemos representar en una gráfica "todos" los puntos [x,f(x)] de una función cuadrática, obtendríamos siempre una curva llamada parábola.
 |
| Parábola del puente, una función cuadrática. |
Como contrapartida, diremos que una parábola es la representación gráfica de una función cuadrática.
Dicha parábola tendrá algunas características o elementos bien definidos dependiendo de los valores de la ecuación que la generan.
Estas características o elementos son:
Orientación o concavidad (ramas o brazos)
Puntos de corte con el eje de abscisas (raíces)
Punto de corte con el eje de ordenadas
Eje de simetría
Vértice
Orientación o concavidad
Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.
Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax2):
Si a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x2 − 3x − 5

Si a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2 + 2x + 3

1.8 Función Exponencial y Logarítmica.
Función Exponencial:
La función f es definida por: f(x)=bx, donde b es mayor a 0, b no es igual a 1, y el exponente x es cualquier número real, se llama Función Exponencial con base.
La función exponencial es del tipo:

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.
Ejemplos


La función logarítmica en base a es la función inversa de la exponencial en base a.


Ejemplos

| x |  |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |


| x |  |
|---|---|
| 1/8 | 3 |
| 1/4 | 2 |
| 1/2 | 1 |
| 1 | 0 |
| 2 | −1 |
| 4 | −2 |
| 8 | −3 |

1.9 Aplicaciones en las ciencias económico administrativas:
funciones de oferta y demanda; recta presupuestal, funciones de ingresos,
costos, y utilidades; funciones de apreciación y depreciación.
Función de Oferta:
Definición de función de oferta y su relación cantidad-precio:
La función de oferta es una expresión matemática que relaciona los precios de un producto con las cantidades que el productor está dispuesto a generar.
Su expresión matemática es la siguiente:
X = F (P ,Ps ,Pc, T ,G ,O)
Donde :
Su expresión matemática es la siguiente:
X = F (P ,Ps ,Pc, T ,G ,O)
Donde :
- P = Precio
- Ps = Precio de productos sustitutivos
- G = Gustos
- Pc = Precio de productos complementarios
- O = otras variables
- T = Tecnología
Dentro de estas variables diferenciamos dos tipos:
- Exógenas : Ps, Pc,G, O, T
- Endógenas : P
La relación cantidad ofertada y el precio del producto, en este caso será POSITIVA
Representación gráfica: (línea roja)
 |
| telarana-8.gif |
Función de Demanda:
Definición de función de demanda y su relación cantidad-precio.
La función de demanda es una expresión matemática que relaciona la cantidad demandada de un bien o servicio con las variables de las que ésta depende.
Su expresión matemática es la siguiente:
X = F (P ,Ps ,Pc ,G ,O)
Donde :
La función de demanda es una expresión matemática que relaciona la cantidad demandada de un bien o servicio con las variables de las que ésta depende.
Su expresión matemática es la siguiente:
X = F (P ,Ps ,Pc ,G ,O)
Donde :
- P = Precio
- Ps = Precio de productos sustitutivos
- G = Gustos
- Pc = Precio de productos complementarios
- O = otras variables
- Exógenas : Ps, Pc,G, O
- Endógenas : P
Representación gráfica:(línea azul)
 |
Recta Presupuestal:
Funciones de Ingresos, Costos y Utilidades:
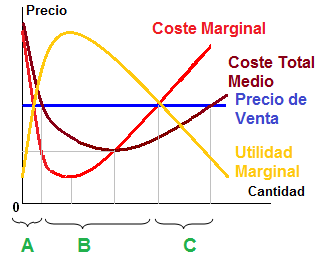
Funciones de Apreciación y Depreciación:
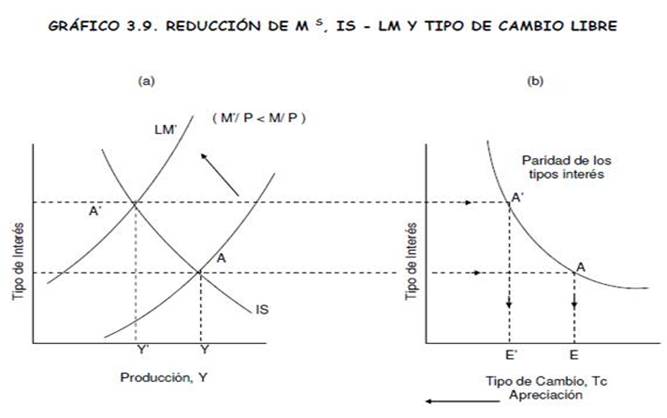
Lo que Aprendí durante la Unidad 1°:
Primero que nada aprendí que era una función, aunque el término ya lo había escuchado, en realidad no sabía ni que era, ni como se obtenía; ya después de que aprendí como era una función, seguí con aprender que una función puede tener dominios y rangos los cuales son como los valores que no puede tomar en una función; aprendí que existen varios tipos de funciones, las cuáles son tan diferentes unas de otras; aprendí a hacer operaciones con funciones con las operaciones básicas como sumar, restar, multiplicar, dividir e incluso operaciones con exponentes y con raíces; vimos como aprender a graficar estas funciones;dentro de las funciones vimos las lineales, las cuadráticas, las exponenciales y las logarítmicas; y al final vimos como se pueden aplicar estas funciones dentro de la vida cotidiana, como para obtener una recta presupuestal, la función de ingreso, costos y utilidades y también las funciones de apreciación y depreciación.















muy buen trabajo! excelente información Migue
ResponderEliminar