viernes, 22 de mayo de 2015

Unidad 4. Tópicos Complementarios de Diferenciación.


4.1 Derivadas de Funciones Logarítmicas.

 Una función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1, puesto que el resultado sería 0.

 La derivada de un logaritmo en base a es igual a la derivada de la función dividida por la función, y por el logaritmo en base a de e.Derivada de una función logarítmica
Como cambio de base, también se puede expresar así:Derivada de una función logarítmica
Video de como Derivar Funciones Logarítmicas:

4.2 Derivadas de Funciones Diferenciables.

Si f(x) es una función derivable, la diferencial de una función correspondiente al incremento h de la variable independiente, es el producto f'(x) · h.
La diferencial de una función se representa por dy.
Diferencial
Diferencial
Interpretación geométrica
Diferencial de una funciónDiferencialDiferencial
La diferencial en un punto representa el incremento de la ordenada de la tangente, correspondiente a un incremento de la variable.

Video de como derivar Funciones Diferenciables:

4.3 Diferenciación Implícita.


   Funciones implícitas
Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.
Derivadas de funciones implícitas
Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:
x'=1.                                                               En general y'≠1.                                                 Por lo que omitiremos x' y dejaremos y'.
Derivar las funciones:
1. Derivación implicita                      Derivación implicita
2. Derivación implicita            Derivación implicita
Video de como realizar la Diferenciación Implícita:                      https://www.youtube.com/watch?v=oneC1gsSQaM
4.4 Diferenciación Logarítmicas.
Con determinadas funciones, especialmente para la función potencial-exponencial, es aconsejable el empleo de la derivación logarítmica, ya que facilitan bastante el cálculo.
       4.5 Derivadas de Orden Superior.    
Si $f$ es una función diferenciable, es posible considerar su función derivada como: 
$f'=\{(x,y)/\;y=D_{x}f(x)\}$ para $x$ en el dominio $M$ de $f$. 
Si para algunos valores $x \in M$ existe el $\displaystyle{\lim_{h \rightarrow{0}}{\frac{f'(x+h)-f'(x)}{h}}}$ se dice que existe la segunda derivada de la función $f$ que se denota por $f''(x)$ o $D_{x}^{2}f(x)$, que equivale a $D_{x}[D_{x}f(x)]$. O sea, la segunda derivada de la función $f$ se obtiene derivando la primera derivada de la función. 
Ejemplos: 
  1. Si $f(x)=5x^{3}+6x^{2}-5x+1$ entonces: $f'(x)=15x^{2}+12x-5$ y 
    $f''(x)=30x+12$ 
  2. Si $\displaystyle{g(x)=\frac{x^{2}+3x}{x-1}}$ entonces: $\displaystyle{g'(x)=\frac{(x-1)(2x+3)-(x^{2}+3x)}{(x-1)^{2}}=\frac{x^{2}-2x-3}{(x-1)^{2}}}$ y derivando nuevamente 
    $\displaystyle{g''(x)=\frac{(x-1)^{2}(2x-2)-(x^2-2x-3)2(x-1)}{(x-1)^{4}}}$
    $=\displaystyle{\frac{(x-1)^{2}(2x-2)-(x^{2}-2x-3)2(x-1)}{(x-1)^{4}}}$
    $=\displaystyle{\frac{(x-1)[(x-1)(2x-2)-(x^{2}-2x-3)]}{(x-1)^{4}}}$ 
    Por tanto $\displaystyle{g''(x)=\frac{8}{(x-1)^{3}}}$ 
Video de como hacer las Derivadas de Orden Superior:

4.6 Diferenciables.

Sea f(x) una función derivable. Diferencial de una función correspondiente
al incremento h de la variable independiente, es el producto f'(x) · h. Se representa por dy.
Diferencial
Diferencial
Diferencial de una función
Diferencial
Diferencial
Video de como solucionar una Ecuación Diferencial:

4.7 Aplicaciones a las Ciencias Económico Administrativas: Costo Marginal, Ingreso Marginal, Utilidad Marginal, Propensión Marginal al Consumo y Propensión Marginal al Ahorro.
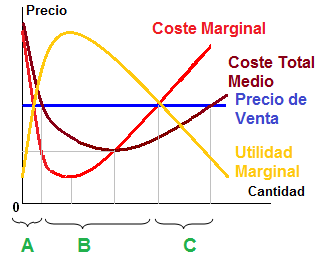
Costo Marginal:

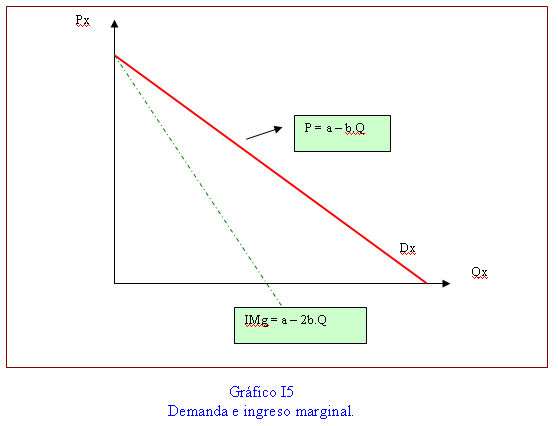
Ingreso Marginal:


Utilidad Marginal:


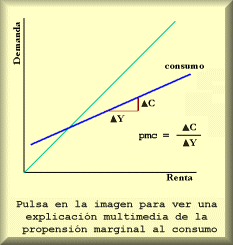
Propensión Marginal al Consumo y al Ahorro:


Lo que aprendí en la Unidad 4°:

En esta unidad aprendí a obtener las derivadas de las funciones logarítmicas y de las funciones exponenciales; después de esto aprendimos a sacar la diferenciación implícita, y la logarítmica; aprendimos a obtener las derivadas de orden superior, y a obtener diferenciales; y al igual que en la unidad 3° vimos como aplicar las derivadas en costo marginal, ingreso marginal y utilidad marginal; propensión marginal al consumo y al ahorro.





                   



Publicado por en

2 comentarios:

Suscribirse a: Enviar comentarios (Atom)