Unidad 2. Límites y Continuidad.

2.1 Definición de Límite.

El límite de f(x) cuando x tiende a a, es el número L, que se escribe lim cuando x tiende a a de la función f(x)=L, siempre que f(x) esté arbitrariamente cercana a L para toda x lo suficientemente cerca, pero diferente de a. Si no existe tal número, se dice que el límite no existe.

El límite de la función f(x) en el punto x₀, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x₀. Es decir el valor al que tienden las imágenes cuando los originales tienden a x₀.

Vamos a estudiar el límite de la función f(x) = x² en el punto x₀ = 2.

x	f(x)
1,9	3,61
1,99	3,9601
1,999	3,996001
...	...
↓	↓
2	4

x	f(x)
2,1	4.41
2,01	4,0401
2,001	4,004001
...	...
↓	↓
2	4

Tanto si nos acercamos a 2 por la izquierda o la derecha las imágenes se acercan a 4.

2.2 Propiedades de los Límites.

Límite de una constante

Límite de una suma

Límite de un producto

Límite de un cociente

Límite de una potencia

Límite de una función

g puede ser una raíz, un log, sen ,cos, tg, etc.

Límite de una raíz

Límite de un logaritmo

                 2.3 Límites Laterales.

Para que exista el límite de una función, deben existir los límites laterales y coincidir.

El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera

• x ® a^- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.

• x ® a⁺ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha.

Límite lateral por izquierda  si dado e > 0, $ d > 0 tal que si a - d < x < a Þ

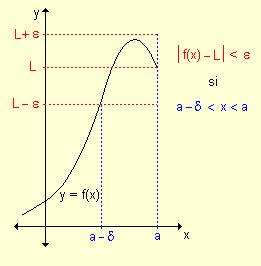Límite lateral por derecha  si dado e > 0, $ d > 0 tal que si a < x < a + d Þ

Observación. Una función tiene límite si los límites laterales son iguales, es decir, cuando 

2.4 Límites al Infinito.

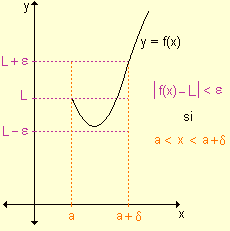Uno entre infinito

Empecemos por un ejemplo interesante.

Pregunta: ¿Cuál es el valor de 1/∞ ?

Respuesta: ¡No lo sabemos!

¿Por qué no lo sabemos?

La razón más simple es que infinito no es un número, es una idea. Así que 1/∞ es un poco como decir 1/belleza o 1/alto.

A lo mejor podríamos decir que 1/∞ = 0 ... pero eso es un poco problemático, porque si dividimos 1 en infinitas partes y resulta que cada una es 0, ¿qué ha pasado con el 1?

De hecho 1/∞ es indefinido.

¡Pero podemos acercarnos a él!

Así que en lugar de intentar calcular con infinito (porque no sacaremos ninguna respuesta razonable), vamos a probar con valores de x más y más grandes:

x 1/x 1 1.00000 2 0.50000 4 0.25000 10 0.10000 100 0.01000 1,000 0.00100 10,000 0.00010

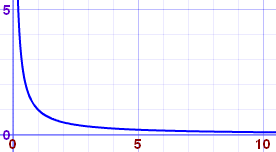Vemos que cuando x crece, 1/x tiende a 0

Reglas para calcular límites al Infinito:

1° Si el exponente más grande está en el numerador su resultado va a a ser + ó - infinito.
2° Cuando el máximo exponente está en el numerador y en el denominador el resultado es los coeficientes que lo acompañan.
3° Cuando el exponente mayor esta solo en el denominador el resultado es 0.

2.5 Continuidad y Discontinuidad.

Continuidad:
Una función f es continua en a si y sólo si se cumplen las siguientes tres condiciones:

1° f(a) existe.
2° lim x tiende a a f(x) existe.
3° lim x tiende a a f(x)=f(a)

Estudiar la continuidad de  en x = 2

1. La función tiene imagen en x = 2.

f(2)= 4

2. La función tiene límite en x = 2 porque coinciden los límites laterales.

3. En x = 2 la imagen coincide con el límite

En la gráfica podemos comprobar que es continua.

Discontinuidad:

Una función es discontinua si:

1) f no tiene límite cuando x tiende a a ó

2) Cuando x tiende a a, f tiene un límite diferente de f(a).

Si alguna de las tres condiciones continuidad de no se cumple, la función es discontinua en un punto.

La función es discontinua porque en x = 2 no existe imagen.

La función es discontinua porque en x = 2 no tiene límite,
ya que no coinciden los límites laterales.

La función es discontinua porque en x = 2 no coincide 
la imagen con el límite.

2.6 Aplicaciones a las Ciencias Económico

     Administrativas: interés compuesto 

     continuamente, límite de la función,

                costo promedio.

Interés Compuesto Continuamente:

Límite de la Función:

Costo Promedio:

Lo que aprendí de la Unidad 2°:

Bueno, en la Unidad 2° aprendí, lo que era un límite, las propiedades del mismo,                                                                                   vimos que existen límites laterales y límites al infinito; también vimos la continuidad                                                                               y la discontinuidad, y como se aplican los límites en el interés compuesto continuo                                                                               y el límite de la función costo promedio.